Power vs Torque Questionnaire -RESULTS

[Phil]

Since you seem to believe that the torque is of significance, where is the flaw of the logic described above? By the way everyone is welcome to answer me.

Torque at the wheel is of significance. Anything other than that is influenced by the transmission and gearing, as we have established before. Torque is no more or less significant than power, since both are directly related and linked with each other through the rpm speed. You can't exclude one from the other.
I think we understand each other. We're just talking around in circles a bit.

I maintain that to determine acceleration, the [power/torque] curve is key. If the curve shows power or torque is not really crucial since both can be derrived from eachother. I guess I just have difficulty deciding between one or the other since both are directly linked with each other. One can not exist without the other...

[Stradivarius]

Since you seem to believe that the torque is of significance, where is the flaw of the logic described above? By the way everyone is welcome to answer me.

Torque at the wheel is of significance. Anything other than that is influenced by the transmission and gearing, as we have established before. Torque is no more or less significant than power, since both are directly related and linked with each other through the rpm speed. You can't exclude one from the other.
I think we understand each other. We're just talking around in circles a bit.

I maintain that to determine acceleration, the [power/torque] curve is key. If the curve shows power or torque is not really crucial since both can be derrived from eachother. I guess I just have difficulty deciding between one or the other since both are directly linked with each other. One can not exist without the other...

We agree on many of the concepts discussed here, but from what you write here, I can't say that we agree on everything. I earlier climed that all of the following information is irrelevant:

-Engine torque
-Engine rpm (absolute figure)
-Gear exchange ratios
-Final drive
-Tyre- and wheel dimensions

And I can also add to this list: The torque at the wheel. You don't need to know it in order to have a complete understanding of a car's performance. A car with smaller torque at the wheels may have a greater motive force than a car with higher torque at the wheels, since the force depends on both the torque and the radius of the wheel.

There is no doubt that you can use irrelevant information in order to determine the key parameters, but as long as you can't go the oposite way from the key parameters to this information, it must be irrelevant, I don't see any way around that. When you are at a restaurant which accepts both cash and creditcars payments, and you need to pay the bill, it doesn't matter if you have cash or not as long as you are able to pay the bill. The potential concern of the restaurant owner is that you can't pay the bill. So even if using cash is one way of paying the bill, it is completely irrelevant to the restaurant owner if you have cash or not. The only relevant issue is whether or not you are able to pay one way or the other. Of course it is possible to use irrelevant information such as "you do have enough cash" in order to conclude on the key issue that you are able to pay. But you can't go the other way. If you tell me that you are able to pay, that is not enough information for me to determine whether you have enough cash or if you're using your credit card.

So I ask again if you think there is any flaw in my logic reasoning. You don't need to refer to the relationship between different parameters, you just need to explain what is wrong with my logic presented in my previous post and elaborated here and elsewhere.

[Phil]

Strad... No offence, but now you are just nit-picking... Radius of the wheel? we were never exactly comparing tractors with cars. btw; radius is considered in the performance app a few pages back - I'm well aware of the correlation. I just wasnt aware i had to go through all lengths to mention it. I think we agree.

[Charlatan]

This thread needs a moderator with proper engineering background, many posts have no technical relevance to the subject.

This should be about science and not a beauty-contest, neither is science a democracy.

[xxChrisxx]

An engineering mod is absent because anyone with an engineering brain knows to avoid a torque vs power thread.

Because they are a waste of --- space.

[J.A.W.]

Those last two posts are really fairly funny.. ..ironic..

Obviously.. the subject is pretty much akin to the Sinatra - 'Love & Marriage' - song,
- as in a balance of the two - being generally essential to proper functioning in each instance..

Was it an ancient Greek who invented the rope & pulley/block & tackle set-up of torque/power/gearing?

[Stradivarius]

Strad... No offence, but now you are just nit-picking... Radius of the wheel? we were never exactly comparing tractors with cars. btw; radius is considered in the performance app a few pages back - I'm well aware of the correlation. I just wasnt aware i had to go through all lengths to mention it. I think we agree.

Yes we do agree for the most. I mentioned the wheel radius because you actually brought it into your calculations in the first place, where they differed by around 1%. This is nothing, as for example ignoring the moment of inertia of the wheels (which we have all done here) typically accounts for an error/inaccuracy of at least 2-3%.

But I don't think it is nit-picking to establish which parameters are relevant and which parameters are not. There is a few things you need to know in order to describe or evaluate the performance of an existing car and torque is not one of them. As explained earlier, and as you have done in your calculations, you can use the torque together with other parameters to derive relevant parameters such as power or motive force, but that doesn't make the torque itself a relevant parameter.

If you are going to design a new car from scratch, there is a lot more things you need to know. You need to dimension all parts of the drive-train, including gears, shafts and bearings, so that they can sustain the loads to which they are going to be exposed. You also need to settle on a final drive exchange ratio that matches the rest of the system and in such considerations, torque is a critical parameter. But we are not designing new cars here. We are only studying the performance of existing cars, so for us the torque is of no significance.

[J.A.W.]

"Torque is of no significance"?

That is analogous to - "sure, oxygen forms an intrinsic % of air - but it is of no significance to lung function"..

It is in fact fundamental to both - torque for shaft hp & O2 for lung function..

[Stradivarius]

"Torque is of no significance"?

That is analogous to - "sure, oxygen forms an intrinsic % of air - but it is of no significance to lung function"..

It is in fact fundamental to both - torque for shaft hp & O2 for lung function..

It's a good analogy: If you already know that a person is breathing fine and not suffocating, there is no need for you to start measuring the concentration of oxygen in the surrounding air to make sure he doesn't die.

Please feel free to point out the flaw in this logic argument:

Premise: It is possible to describe the car- or engine performance completely without knowing the torque and without having the information necessary to determine the torque.

Logical conclusion: The torque is not of any significance when it comes to car- or engine performance.

Reasoning: If the torque was of any significance regarding car- or engine performance, the premise would be false. It wouldn't have been possible to describe the car- or engine performance completely without knowing the torque or having the information necessary to determine the torque.

[Richard]

As a mod it seems the thread has been well behaved and Machin is more than capable of explaining simple physics. Also it's self evident that the questionnaire and discussion was inevitably going to prompt someone to disagree.

As for the simple physics, the Merc example shows that MB have cunningly engineered both diesel and petrol engines to give very similar performance at the wheel as shown below:



This is because the crankshaft/flywheel power curves have a very similar shape albeit scaled differently on the x axis (ie RPM).

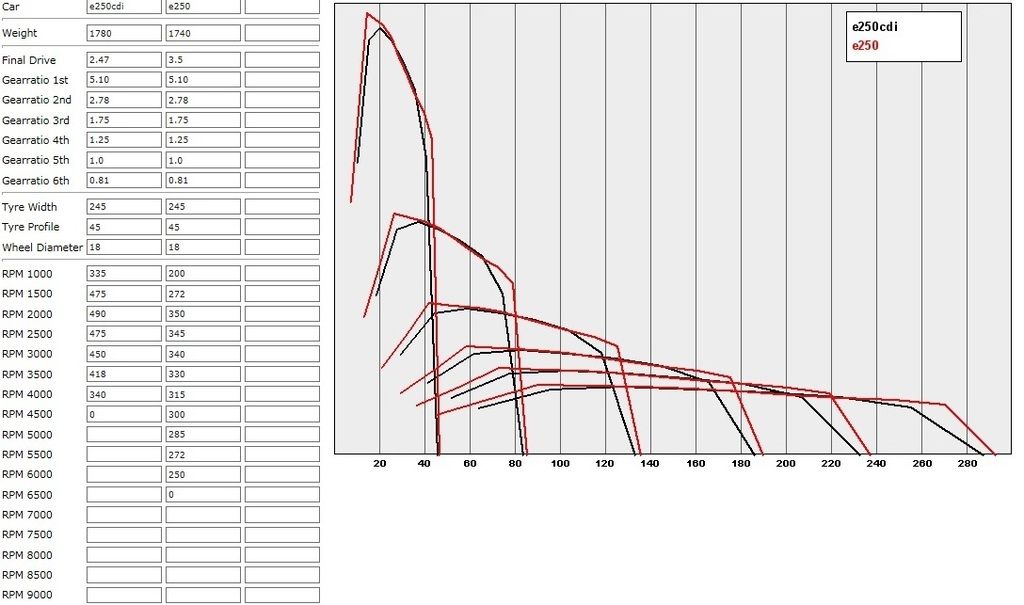
All Machin is saying is that using torque at the crankshaft is meaningless when assessing a car's performance. A hamster on a treadmill could generate the same torque as an F1 engine given suitable gearing. However a hamster doesn't have the same power as an F1 engine.

[machin]

But the peak torque figure still tells us at which point the engine, from a mechanical stand-point, produces the max turning force. A bit like when you are on a bicycle riding away - there is a point of speed at which you pedle where you have the best turning force. It's not the maximum rev and it wouldn't be where you are producing the max "power".

Well, as cycling is mentioned again.... Actually this gives a us a good example of why a power curve is much more useful than a torque curve.... As I said before, I'm a "keen" (aka "obsessed") cyclist, and every ride I do is logged... I literally have torque/power/rpm data for over 3 million pedal strokes, and this allows me to construct a curve of my torque (at the pedals), in this case for my best output over 30 seconds (more than 30 seconds and the torque drops off as I fatigue)



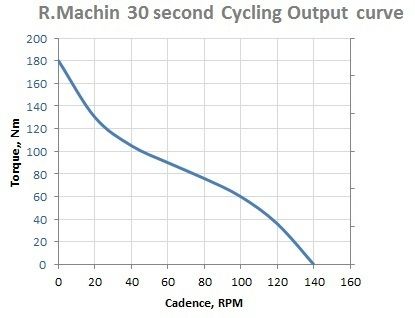
As you can see the torque curve drops off with increasing RPM... you can prove this relationship: Standing still with the rear brakes on you can put huge torque into the cranks by pushing down with one leg (using your arm muscle to react against the handlebars) and pulling up with the other... and in the other extreme you can lift the rear wheel off the ground and see how fast you can spin your legs without reacting against any resistance.

Earlier in this thread i presented the following equation:-

Top speed is achieved when ((Crankshaft torque x gear ratio)/(Driven Wheel radius)) = (Resistance Forces)

Now lets say I want to climb a hill as fast as I can, the question is, what cadence (and hence gear) should I use to get me to the top as fast as possible?

Should I pedal at the speed with highest pedal torque? Clearly not as that is 0rpm and isn't going to get me anywhere!

Should I pedal at the highest possible pedal speed? No because then I'm generating no torque at all...

Remembering that overall gear ratio is just Crank (or pedal) RPM / Wheel RPM, we can substitute as follows:

(((Crankshaft torque) x (Crank RPM)/(wheel RPM))/(Driven Wheel radius)) =(Resistance Forces)

So it is clear that to maximise motive force for a given road speed (and hence speed up my hill) we need to maximise the value of Crank Torque x Crank RPM.... which is very difficult to see from the torque curve above....

...So lets put some values on a few points:-



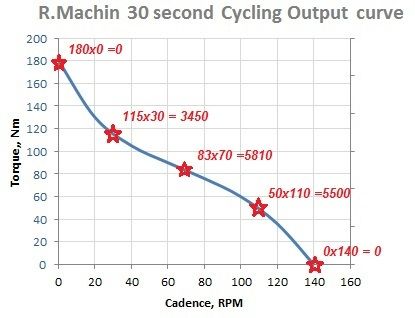
We can now see that my peak Pedal Torque x RPM occurs somewhere in the brackets 70 to 110rpm...

And if we Plot (Pedal Torque x RPM) across the full range of RPM we get this chart:



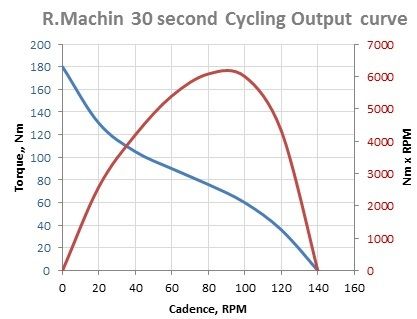
Now we can see instantly that the best RPM I should use for climbing my hill is about 90rpm, or at the very least somewhere between 80 and 100rpm.... So next time I am climbing a hill and pushing as hard as I can, but only achieving a cadence of 60rpm, I know I should change down to bring my cadence up to 90rpm, (but I still need to be pushing as hard as I can at that RPM, but it will be a little less than before).

The red curve in the chart above is my "power" curve, and can be converted from (Nm x RPM) to watts by dividing by 9.55. Which gives me a peak power output over 30 seconds of about 620 watts.

[Tim.Wright]

Interesting, how are you logging torque?

[machin]

Interesting, how are you logging torque?

Measured using crank mounted strain gauges, and recorded on a Garmin GPS head unit.

[Richard]

in this case for my best output over 30 seconds (more than 30 seconds and the torque drops off as I fatigue)
...
Now lets say I want to climb a hill as fast as I can, the question is, what cadence (and hence gear) should I use to get me to the top as fast as possible?

A minor pedantic point - Your 30 second dataset would be useful for a sprint, but you'd burn out if you used that data to determine the optimum RPM for long climb.

[machin]

Agreed.

I used that time duration because the cycling data I posted earlier in this thread had my average output over a short (but steep) hill outside my house which takes 30 seconds flat-out to climb (just over a minute normally).

My power output over an hour also peaks at about 90rpm, but this time the torque is about half the 30 second value... so I can hold 300watts; either way 80-90 rpm is where I generate the most power for pretty much any reasonable time duration.